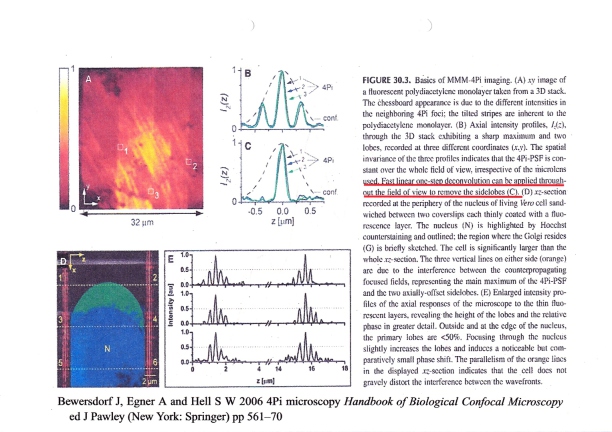
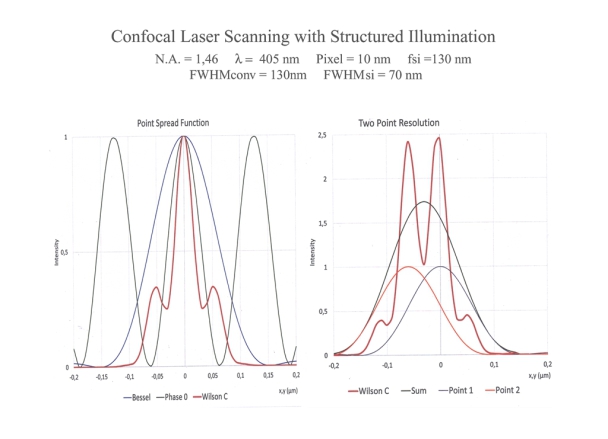
Information and Method
Today, the dimensions of the smallest objects of a semiconductor circuit and the diameter of the dendrites of the human nerve cells are not only of the same order of magnitude but almost equal to 20 nm. The difference lies in the density of the structures. The distance between the objects of the semiconductor circuit can be down to 20 nm.
The distance between the dendrites is significantly greater. This makes it possible to make dendrites visible, even with a coarser resolution than 20 nm. This should be done using a 2-beam interference microscope.
The improvement of the signal-to-noise ratio is of great importance without affecting the object. Simultaneous recording for the Structured Illumination signals is possible with sufficient signal to noise.
With conservative (Full Field) Structured Illumination and near UV, a point spread function in X, Y and Z of around 60 nm (FWHM) is expected. This value should be significantly reduced for Structured Illumination and laser scanning.
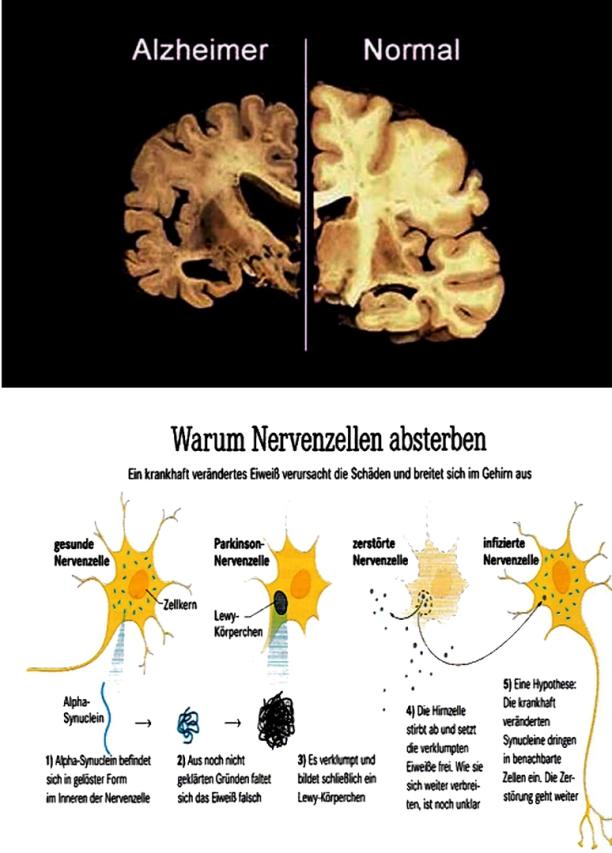
This is a good prerequisite for the measurement of small objects in the brain by signal height. This could make it possible to detect brain diseases earlier.
Nervous Diseases
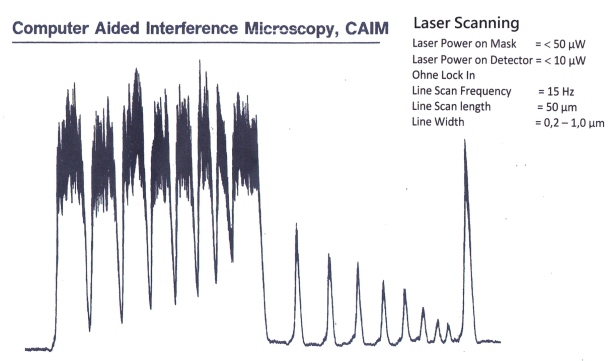
Computer Aided lnterference Microscopy, CAIM
Microscope Set-up
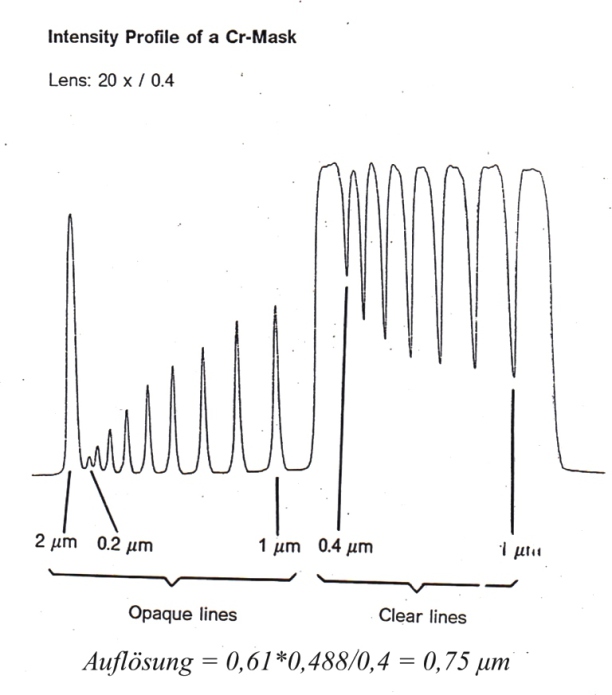
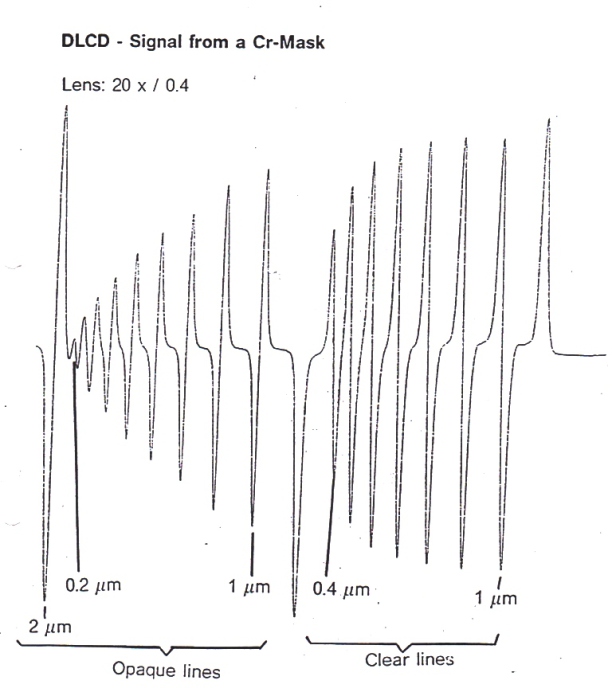
Limits of a E-Beam Mask Writing System
Semiconductor Manufacturing 1988
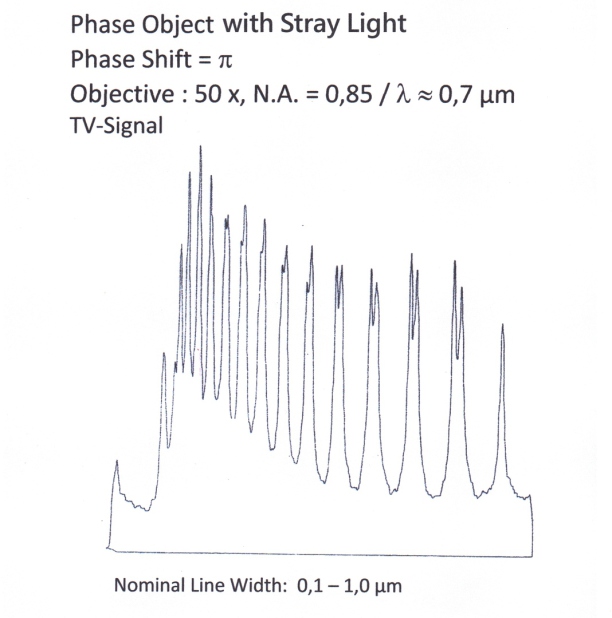
Cr-Mask with lines from 0,2-1,0 μm width
Objective: 50x / 0,95
Grating Modulation
M. Lacombat et al., Solid State Technology/ August 1980
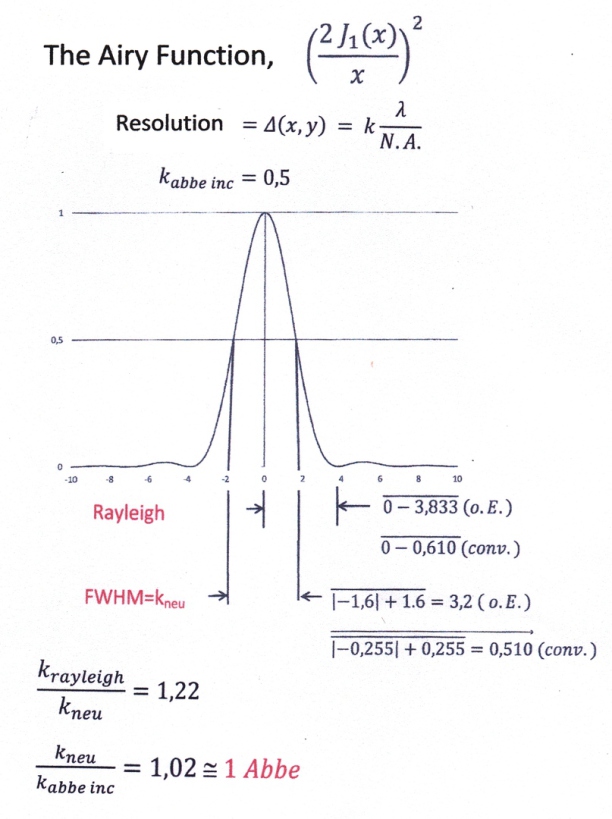
The Airy Function
Computer Aided lnterference Microscopy, CAIM
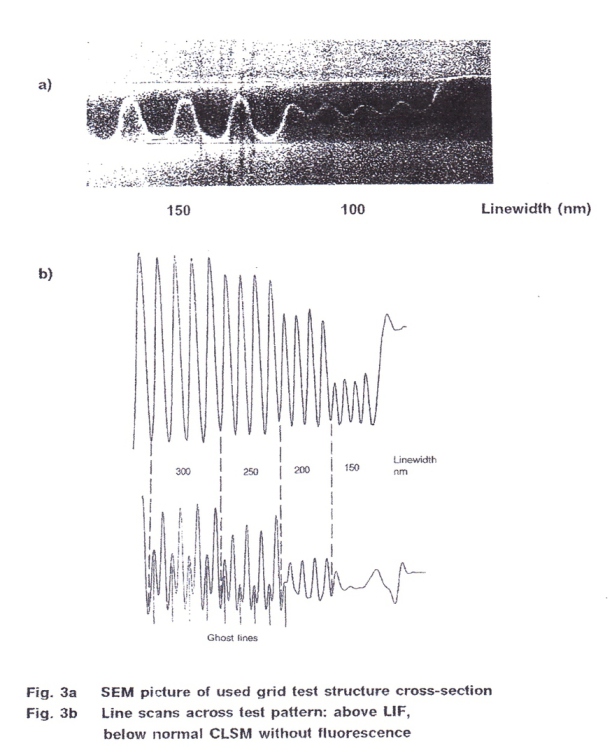
DLCD - Digital Line Center Detection
Conventional Linewidth Measurements
Signal Height vs Linewidth
DLCD - Digital Line Center Detection
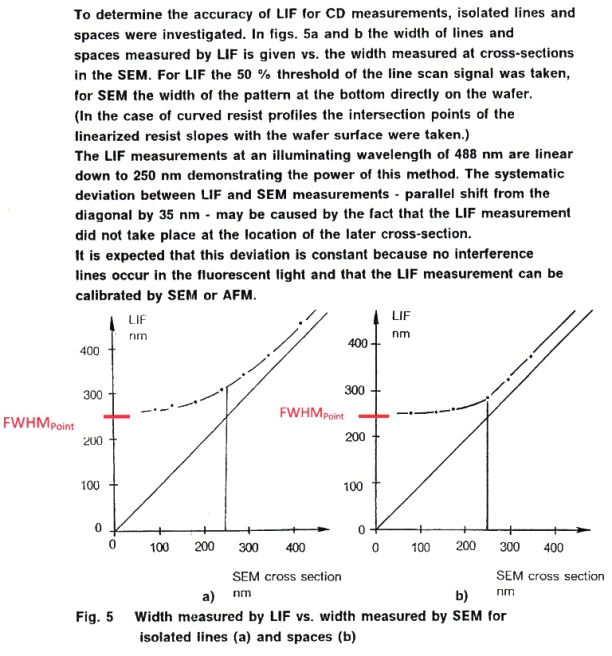
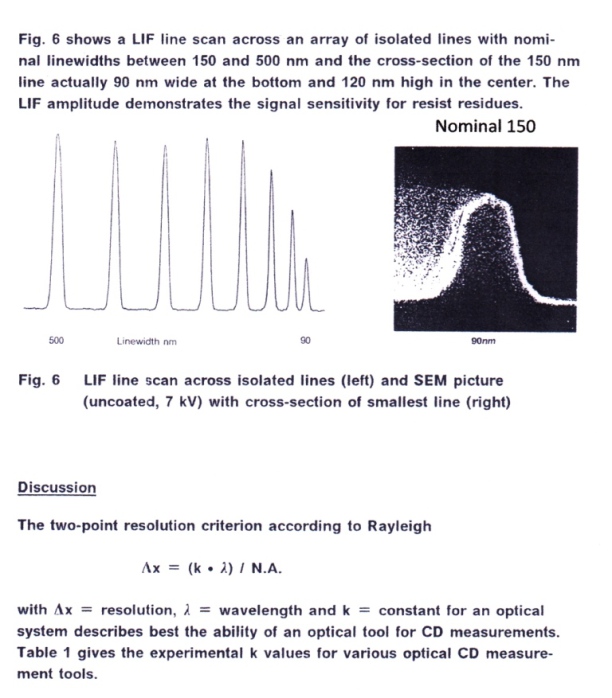
Light-lnduced Fluorescence
Light-lnduced Fluorescence,1992
Testwafer with 360 nm Thick Resist Lines and Dots from 100nm to 500 nm
Computer Aided Interference Microscopy, CAIM
Test Wafer with Structures in 360 nm Thick Resist
Lines Perpendicular and Parallel to Wollaston Split
N.A. =0,85,
λ =700 nm,
Magnification = 3 600 x
Lines and Dots nominal from 100 to 1 000 nm
Smallest Visible Line = 100nm, k =0,12
Smallest Hardly Visible Dot =200 nm, k = 0,24
Differential lnterference Contrast, DIC
Kohärente Digitalmikroskopie. KDM
Symmetrical Darkfield for lnspection, SDI +
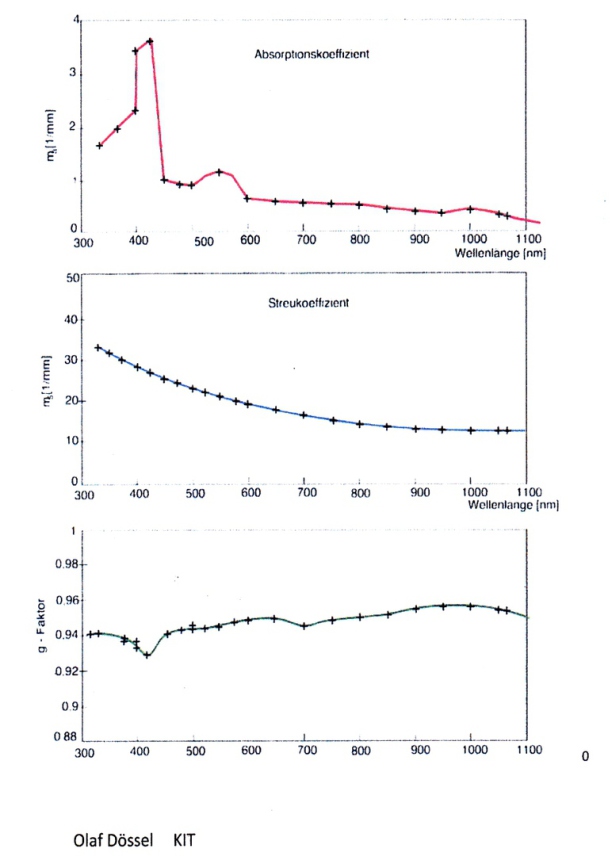
Optical Constants of White Brain Tissue
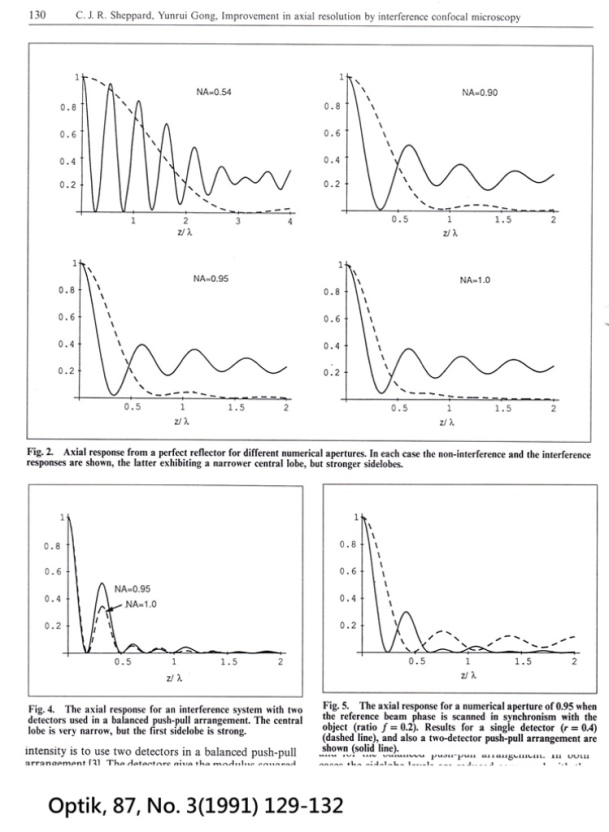
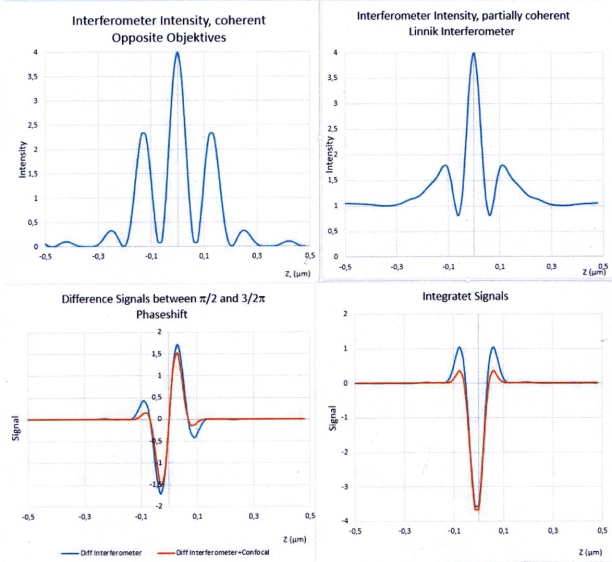
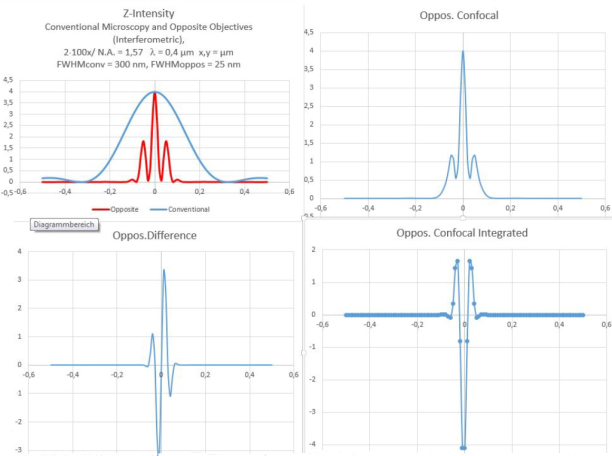
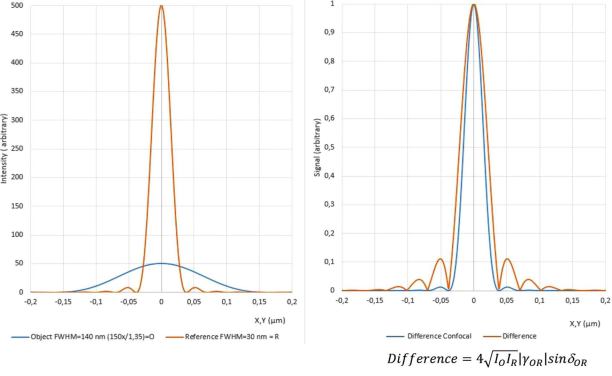
Two Beam Confocal lnterference
Intensity Gain - Linnik-Interferometer
Three Beam lnterference
Virtual Phase Shift - Super Position of two Circular Oscillations
Conclusion:
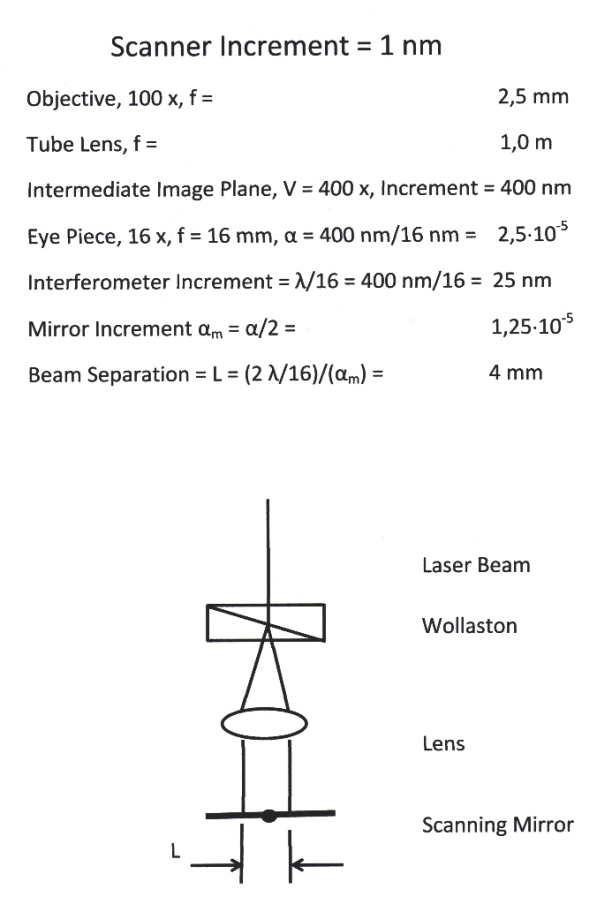
Phase Difference
» Rotation of the Polarization Plane Virtual Phase Shift
» Rotation of the Polarizer
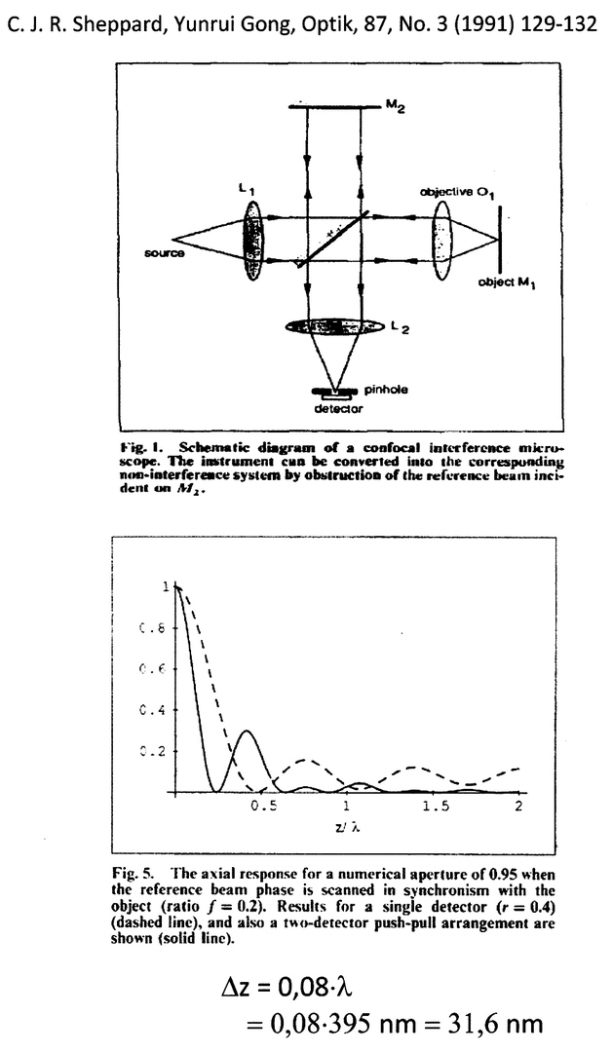
Improvement in axial resolution by interference confocal microscopy
Linnik-lnterferometer, Signals
Axial Differential Interference Contrast, ADIC
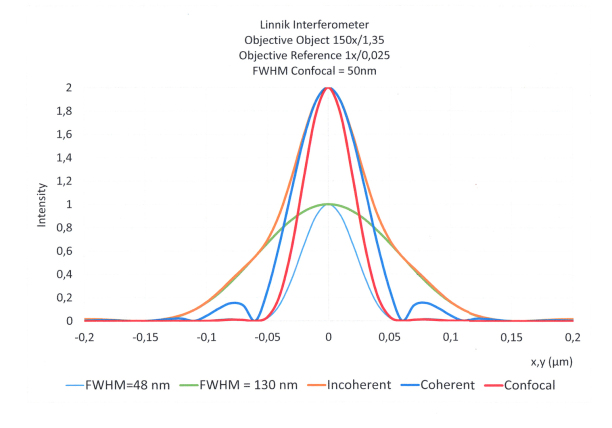
Linnik Interferometer
Linnik Interferometer
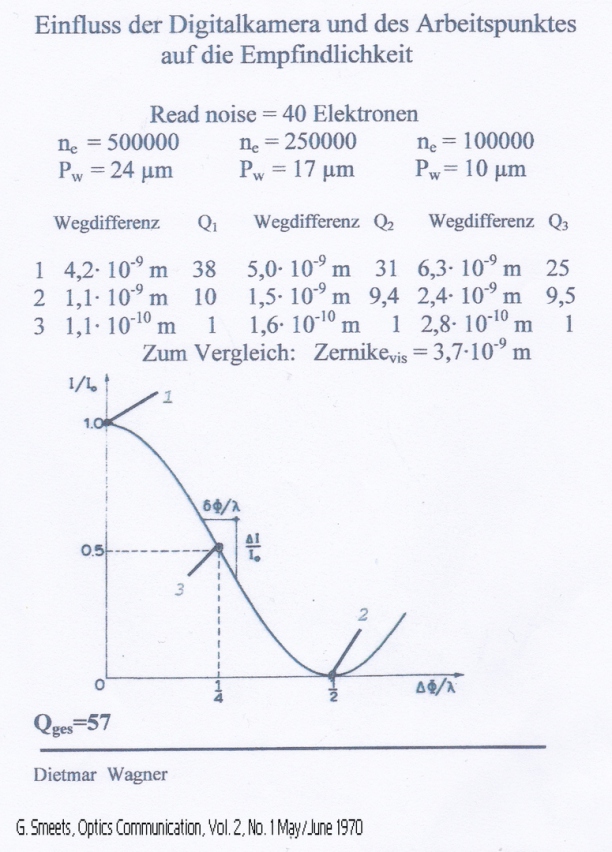
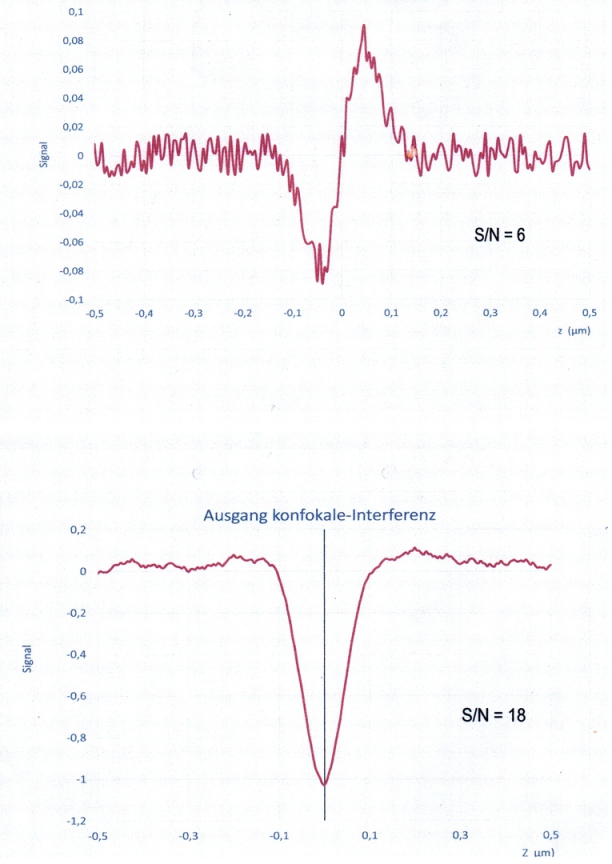
Quantum Signal to Noise
Signal+Noise konfokale Interferenz
Useful Photons/Pixel sec
Optical Point Spread Functions
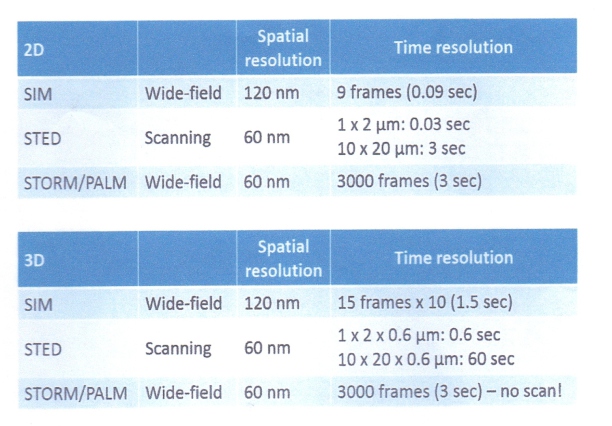
Comparison of time resolution
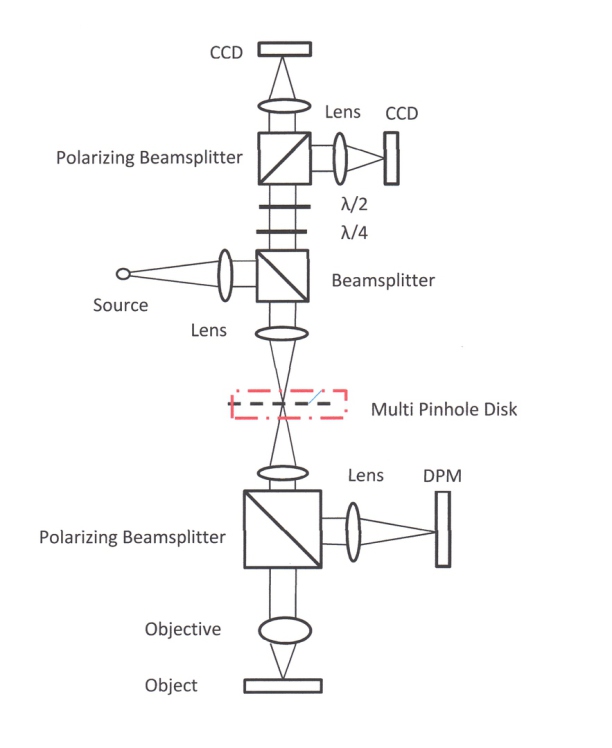
SI- Confocal- lnterference-Microscope (Full Field)
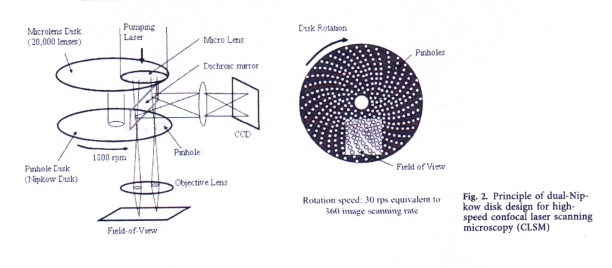
Dual Disk (Real Time) High-Speed Confocal Microscope
Jae Sung Park, Experiments in Fluid 37 (2004) 105-119
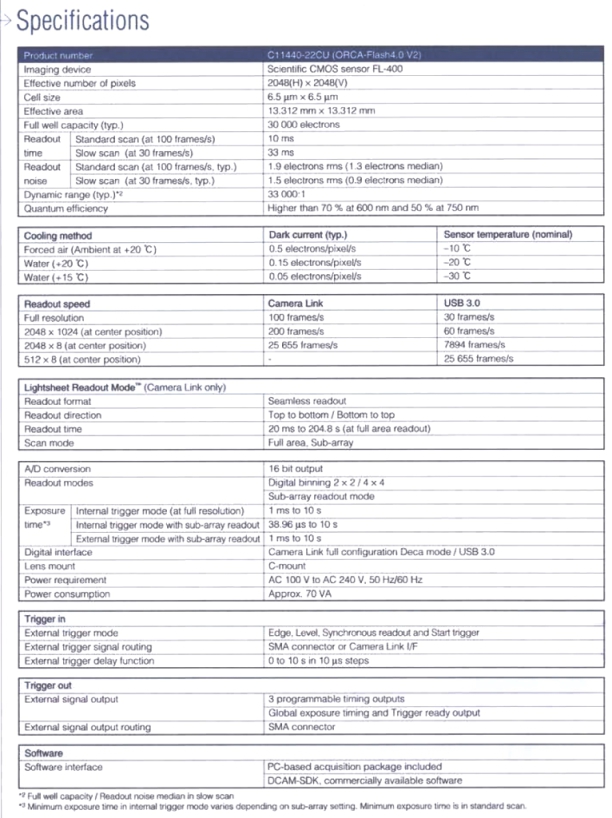
ORCA-Flash 4.0 V2
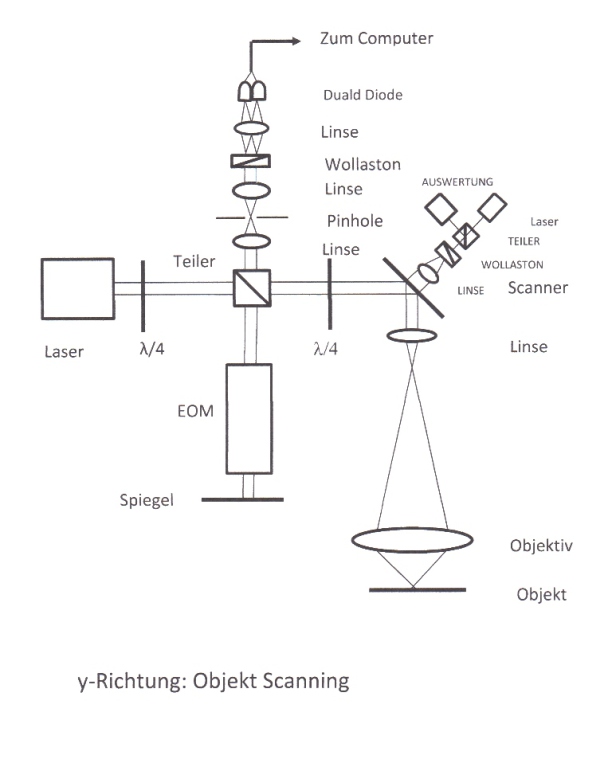
Optical design Laser scanning
Forward-Backward Counting
Confocal interference
Optical Signal Evaluation
Pixels with structured lighting
Method of obtaining optical sectioning by using structured light in a conventional microscope
Structured Illumination by Laser Scanning
Additional References
M. Born, Optik, 1933, Springer Berlin
P. H. van Cittert, Die wahrscheinliche Schwingungsverteilung in einer von einer Lichtquelle direkt oder mittels einer Linse beleuchteten Ebene, Physica,1(1934)
F. Zernike, The Concept of degree of coherence and its application to optical problems, Physica V, No. 8, (1938)
H. H. Hopkins, The concept of partial coherence in optics, Proc. Roy. Soc. (London) A208, (1951)
G. Nomarski, Nouveau dispositif pour l observation en contraste de phase differential, Journal de Physique et Radium, 16, (1955)
M. Born and E. Wolf, Principles of optics, Pergamon Press (1959)
L. Mandel, Concept of cross-spectral purity in coherence theory, JOSA, Vol. 51,
No. 12, (1961)
J. Perina, Coherence of light, Van Nostrand Reinhold Company, London, (1972)
T. R. Corle et al. Depth response of confocal optical microscopes, Optics Letters, Vol. 11, No. 12, (1986)
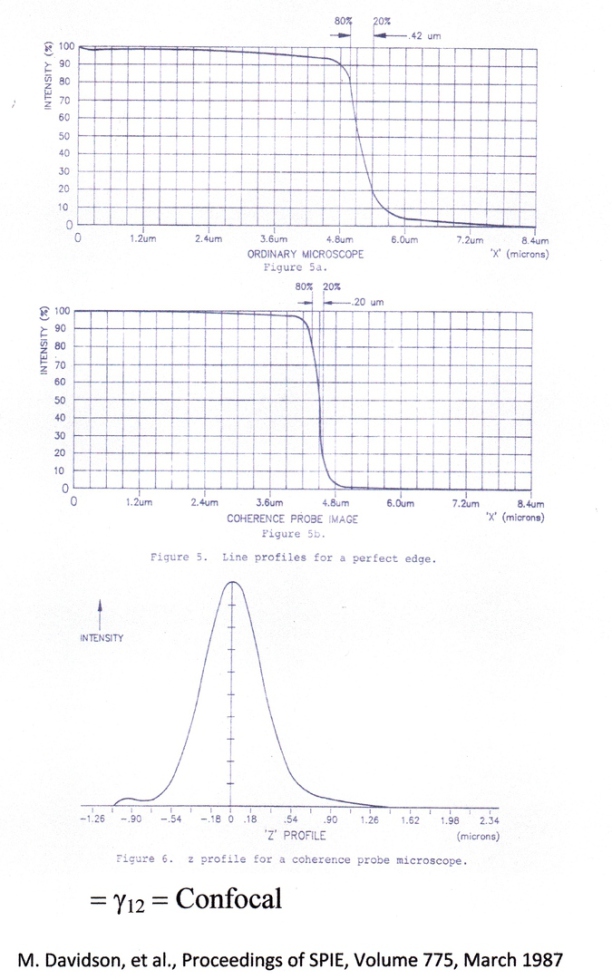
M. Davidson et al. An application of interference microscopy to integrated circuit Inspection and metrology, Proceedings of SPIE, Vol. 775, (1987)
K. G. Larkin, Efficient nonlinear algorithm for envelope detection in white light interferometry, JOSA, A/Vol. 13, No.4, (1996)
M. A. A. Neil, Method of obtaining optical sectioning by using structured light in a conventional microscope, Optics Letters, Vol. 22, No. 24(1997)
M. G. L. Gustafsson, Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy, Journal of Microscopy, Vol. 198, Pt 2, (2000)
L. Schaefer et al. Structured illumination microscopy: artefact analysis and reduction utilizing a parameter optimization approach, Journal of microscopy, TOC, Vol. 216, Issue 2, (2004)
Jianling Chen et al. Super-resolution differential interference contrast microscopy by structured illumination, Optics Express 112,Vol. 21, No. 1 (2013)
Dan Dan, et al. DMD-based LED-illumination super-resolution and optical sectioning microscopy, Scientific Reports; 3 (2013)
Kwanghun Chung et al., Structural and molecular interrogation of intact biological systems, Nature 1, Vol. 000,( 2013)
Mutual Contributions, MC
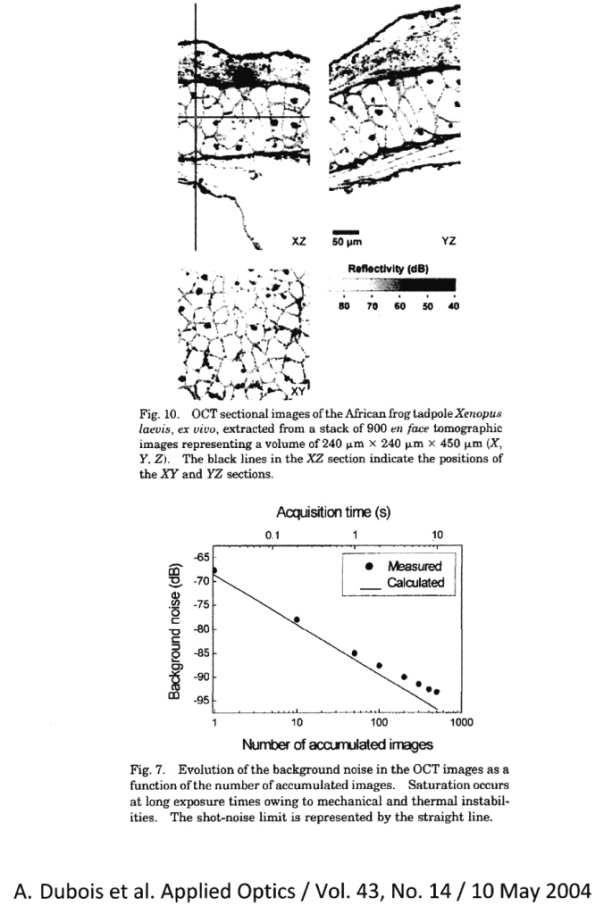
Optical Coherence Tomography, OCT (Spatial)
Don’t work, because of complete light pipes
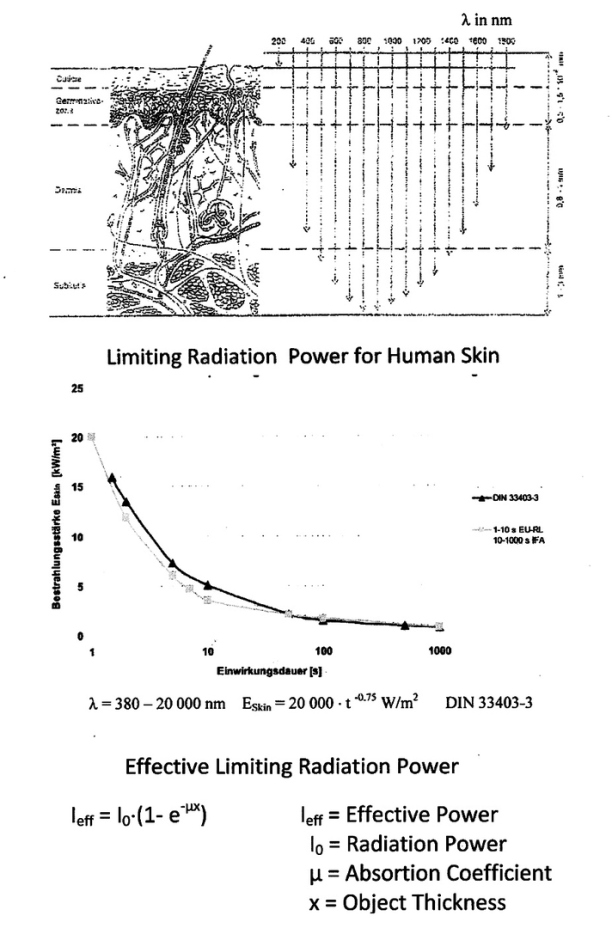
Effect of Optical Radiation in Human Skin
Depth of Radiation in Skin
Optical Coherence Tomography, OCT (Temporal)
Optical Coherence Tomography, OCT (Spatial)
Optical Coherence Tomography, OCT (Spatial)
Principles of Optics - Partially Coherent Light
Point Spread Functions
Two Beam Coherent Source Linnig Interferometer Microscope
Structured Illumination
´Advanced´ Structured Illumination
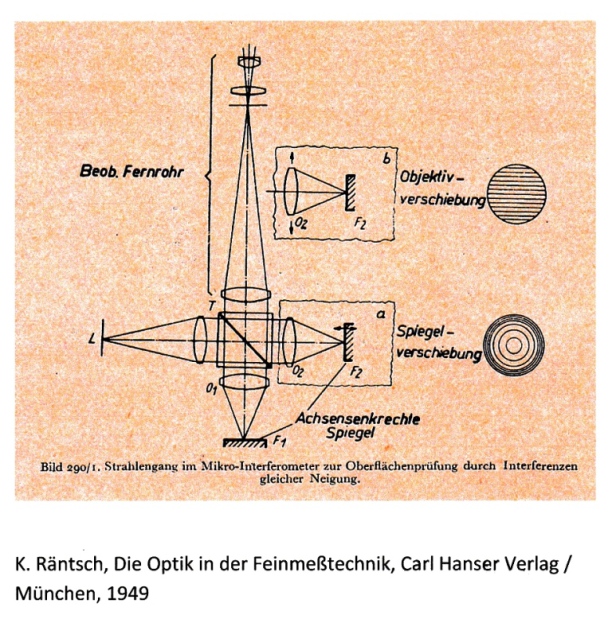
High Resolution Interferometer Microscope
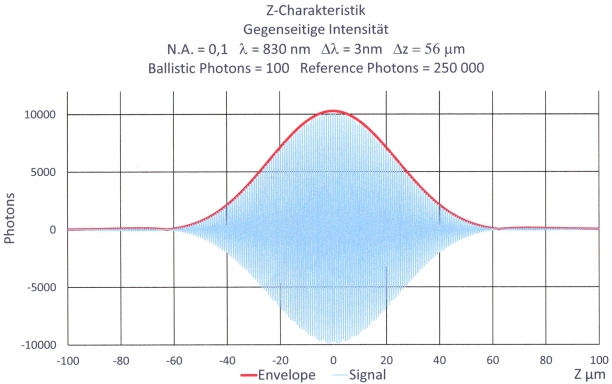
Z-Characteristics
Hier finden Sie uns
Dipl.-Ing. (FH) Dietmar Wagner
Rettistr. 5
70736 Fellbach
Kontakt